Algoritma K-Means Clustering

K-means merupakan salah satu metode clustering non hirarki yang berusaha mempartisi data yang ada ke dalam bentuk satu atau lebih cluster. Metode ini mempartisi data ke dalam cluster sehingga data yang memiliki karakteristik yang sama dikelompokkan ke dalam satu cluster yang sama dan data yang mempunyai karateristik yang berbeda di kelompokan ke dalam cluster yang lain. Secara umum algoritma dasar dari K-Means Clustering adalah sebagai berikut :

1. Tentukan jumlah cluster

2. Alokasikan data ke dalam cluster secara random

3. Hitung centroid/rata-rata dari data yang ada di masing-masing cluster

4. Alokasikan masing-masing data ke centroid/rata-rata terdekat

5. Kembali ke Step 3, apabila masih ada data yang berpindah cluster atau apabila perubahan nilai centroid, ada yang di atas nilai threshold yang ditentukan atau apabila perubahan nilai pada objective function yang digunakan di atas nilai threshold yang ditentukan

Distance space digunakan untuk menghitung jarak antara data dan centroid. Adapun persamaan yang dapat digunakan salah satunya yaitu Euclidean Distance Space. Euclidean distance space sering digunakan dalam perhitungan jarak, hal ini dikarenakan hasil yang diperoleh merupakan jarak terpendek antara dua titik yang diperhitungkan. Adapun persamaannya adalah sebagai berikut :

dimana :
d_ij = Jarak objek antara objek i dan j 

P  = Dimensi data

X_ik = Koordinat dari obyek i pada dimensi k

X_jk        = Koordinat dari obyek j pada dimensi k

  Adapun contoh implementasinya adalah sebagai berikut :

Diberikan data Body Mass Index (BMI) dan ukuran kerangka 20 orang mahasiswa sebagai berikut :

Selanjutnya  kita mencoba mengelompokkan data tersebut di atas menjadi 3 kelompok. Dengan menggunakan algoritma K-Means, berikut langkah - langkah penyelesaiannya :

• Menentukan jumlah cluster, dimana jumlah cluster = 3
• Mentukan pusat cluster secara acak. Disini kita tentukan kita tentukan c1 = (20,9); c2 = (23,10); dan c3 = (27,11).
• Menghitung jarak setiap data yang ada terhadap setiap pusat cluster.  Berikut perhitungannya dengan menggunakan persamaan Euclidean Distance Space :

             - Jarak antara data mahasiswa pertama dengan pusat cluster pertama

             - Jarak antara data mahasiswa pertama dengan pusat cluster ke-dua

             - Jarak antara data mahasiswa pertama dengan pusat cluster ke-tiga

               Adapun hasil dari perhitungan dari keseluruhan data terhadap tiap pusat cluster awal disajikan pada tabel berikut

Menentukan cluster dengan jarak terdekat pada masing-masing data. Adapun hasilnya ditampilkan pada tabel di bawah ini :

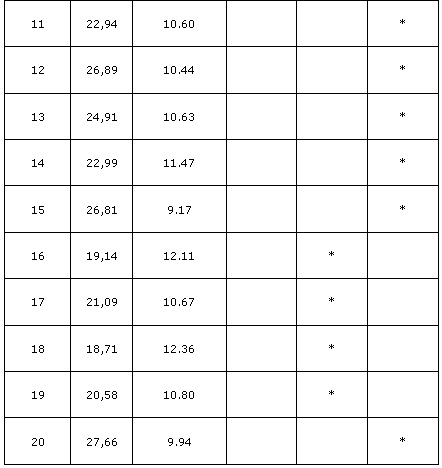
Tabel  iterasi 1

Hitung pusat cluster baru. 

Untuk cluster pertama, ada 4 data yaitu data ke-5, 6, 7 dan data ke-10, sehingga:

- C11 = (17,93+17,72+18,71+18,42) / 4 = 18,19
- C12 = (12,85+12,00+11,53+11,20) / 4 = 11,89
Untuk cluster kedua, ada 7 data yaitu data ke-3, 4, 9, 16, 17, 18 dan data ke-19, sehingga :

- C21  = (19,71+21,05+19,15+19,14+21,09+18,71+20,58) / 7 = 19,92
- C22 = (10,93+10,38+11,8+12,11+10,67+12,36+10,8) / 7 = 11,29

Untuk cluster ketiga, ada 9 data yaitu data ke-1, 2, 8, 11, 12, 13, 14, 15 dan data ke-20, sehingga
- C31 = (22,21+43,25+25,86+22,94+26,89+24,91+22,99+26,81+27,66) / 9 = 27,06
- C32 = (11,64+8,95+9,33+10,6+10,44+10,63+11,47+9,17+9,94) / 9 = 10,24

• Ulangi langkah 2 (Hitung jarak setiap data yang ada terhadap setiap pusat cluster), 3 (Tentukan cluster dengan jarak terdekat pada masing-masing data) dan 4 (Hitung pusat cluster baru)hingga posisi data terhadap cluster sudah tidak mengalami perubahan.

Sumber :
K-Means - Penerapan, Permasalahan, dan Metode Terkait (Yudi Agusta, PhD : 2007)
http://www.megenep.com